Research

It is said that a picture is worth a thousand words. Above, you can see a picture of words (not a thousand, though) that summarizes my current and past research interests. It was generated automatically using Tagul, which takes a body of text as input, and returns a cloud of words as output. Whether a word appears in the generated image or not, depends on the frequency with which that word appears in the input text. The higher the frequency of a word, the more likely it is that it appears in the generated image.
The image above is the result of counting the frequency of the words that appear in my publications page (as of January 2014).
My Research Program
How should a society be organized so that all of its members have appropriate shelter, enough food, and a meaningful role to play? This question has occupied humanity for centuries and, in view of the current state of affairs, we have yet to find a satisfactory answer to it. Interestingly, animals that we normally do not think of as being very intelligent, like ants, bees, or termites, have successfully solved this problem. In fact, insect societies have found ways to deal with problems that are far more complex than any of its members’ cognitive and physical capabilities. How is this possible? How can large groups of relatively simple individuals without central or hierarchical control collectively solve problems? What are the principles and mechanisms that make this phenomenon possible? To what extent discoveries about the problem solving behavior of networks of simple agents can be transferred to the human world in order to tackle social, economic, engineering, and technological problems? What are the limits of this approach?
My research is aimed at addressing the aforementioned questions with an emphasis on the solution of engineering and technological problems. Therefore, my research lies at the intersection of two disciplines: artificial intelligence and complex systems. This intersection has become a field by itself with archival journals and regular specialized conferences exclusively devoted to it. This field is known as swarm (or collective) intelligence.
On the one hand, I am interested in solving problems of practical relevance by using, extending, or developing techniques that are traditionally within the scope of artificial intelligence research, such as search algorithms, neural networks, support vector machines, Bayesian networks, etc. On the other hand, I am interested in the macroscopic spatio-temporal patterns that arise in systems composed of a multitude of interacting entities, for example, bird flocking, vehicle traffic, or the coherent emission of light in lasers. These interests are the foundation of an interdisciplinary research program with two broad goals: a) to understand the principles and mechanisms underlying collective phenomena in order to improve, design, or analyze artificial intelligence systems based on networks of agents, and b) to exploit artificial intelligence techniques to better understand engineered, social and natural complex systems.
Philosophical Foundations
There are no universally-accepted definitions of intelligence and complexity. Nevertheless, any group researching these topics must have working definitions that allow them to make progress. For me, intelligence is a set of skills (e.g., learning, predicting, optimizing, planning, and others) that allows an entity to autonomously solve problems. Regarding complexity, I use of the label complex to refer to systems composed of many entities that interact with each other, often in stochastic and nonlinear ways, through a dynamic network. Typically, a complex system’s components’ behavior and their interaction network are mutually dependent. This means that a component’s behavior depends on which other components it interacts with, and at the same time, the network’s topology depends on the components’ behavior. Hence, the spatio-temporal organization that a complex system exhibits at the macroscopic level cannot be exclusively ascribed to either the system’s components or their interaction network.
Intelligence and complexity have been studied independently of each other until relatively recently. The trigger for a common approach to the study of these phenomena has been the observation that aggregates of humans, animals, or artifacts can behave as a single entity with its own intelligence (or lack thereof) (Le Bon, 1895; Miller, 1921; Grassé, 1959; Beni and Wang, 1993; Bonabeau et al., 1999; Surowiecki, 2005; Seeley, 2010). This observation has led some researchers to propose the idea that intelligence may actually be the result of networks of interacting entities, which can be neurons, people, animals, software agents, or robots (Minsky, 1986; Couzin, 2007; Trianni et al., 2011). From this point of view, which I am going to refer to as the intelligence-as-a-complex-system hypothesis, intelligence and complexity are intimately related.
A research program based on the intelligence-as-a-complex-system hypothesis is both promising and challenging. The great promise is that if the hypothesis is correct, then it should be possible to build intelligent systems made of simple interacting agents. Improvements in a system’s problem-solving capabilities, measured in terms of better performance, greater flexibility or enhanced fault-tolerance, could then be obtained by simply adding more agents to the system. The main challenge, however, is dealing with the complex system (or network) control problem, which consists in knowing a system’s desired collective-level behavior but ignoring exactly what the behavior and interactions of the lower-level system’s components should be in order for the desired macroscopic behavior to emerge.
Evidently, there are complex phenomena that are not directly related to intelligence. For instance, gene expression regulation, firefly synchronization, or traffic jams. Their study, however, is of great importance because understanding these and other systems may help us find unifying principles and mechanisms of complex systems that are applicable to the design of artificial intelligence systems. In the quest to understand complex systems, different tools and techniques, including those that are under the artificial intelligence umbrella, have been used and new ones are being developed. In this sense, artificial intelligence techniques are used, and will continue to be used, to help us better understand complex systems. In summary, swarm intelligence is a two-way knowledge-exchange channel through which artificial intelligence and complex systems can co-develop.
Contributions
Search & Optimization is the artificial intelligence subfield in which swarm intelligence has been most successful. Two techniques stand out: Ant Colony Optimization (ACO) (Dorigo and Stützle, 2004) for tackling combinatorial optimization problems, and Particle Swarm Optimization (PSO) (Kennedy and Eberhart, 1995) for dealing with continuous optimization problems. In both of these techniques, a solution to an optimization problem emerges over time as a result of interactions among simple agents that “move” in a parameter space that is mapped onto the actual feasible solution set of the optimization problem at hand. In ACO and PSO, swarm agents imitate each other inducing a positive feedback process that translates into exploration around promising solutions. My main contributions to the search and optimization subfield can be seen as belonging to one of the following categories: investigations to improve our understanding of swarm intelligence techniques for search and optimization, and performance improvements of swarm intelligence optimization algorithms. Representative publications of the first category are (Montes de Oca et al., 2006; Montes de Oca and Stützle, 2008a,b; Montes de Oca et al., 2009a,b; Liao et al., 2012), in which the behavior of ACO and PSO algorithms are studied in depth. These studies provided insights for proposing a number of performance improvements (Montes de Oca et al., 2009b, 2011b; Liao et al., 2011; Montes de Oca, 2013a) that belong to the second category. Two algorithms in particular are now state of the art for large-scale continuous optimization (Montes de Oca et al., 2011) and mixed-variable optimization (Liao et al., 2013).
Further info:
Ant Colony Optimization (ACO) is an optimization metaheuristic inspired by the foraging behavior of ants. It is based on stigmergy which is an indirect kind of communication that happens through the environment. Real ants communicate through chemicals laid on the ground to recruit other members of the colony to exploit a food source. Artificial ants in ACO bias the search of other ants through some kind of stigmergic communication in the search space. ACO has been shown to be a good optimization technique for hard combinatorial optimization problems. For more information go to Marco Dorigo's Ant Colony Optimization page.
Particle Swarm Optimization (PSO) is a continuous optimization technique inspired by social cognition theories and collective behaviors exhibited by some animals such as birds or fish. In PSO, each individual (called a particle) represents a solution to a continuous optimization problem. Associated with each particle, there is a velocity vector that changes according to its own best past performance and that of its neighbors. In this way, particles ``fly'' over a solution space resembling the movement of insects in a swarm. PSO has captured the interest of a growing research community apparently because it is conceptually simple, technically easy to implement, and has been successfully applied to many problems. For more information go to the publications section.
|
|
|
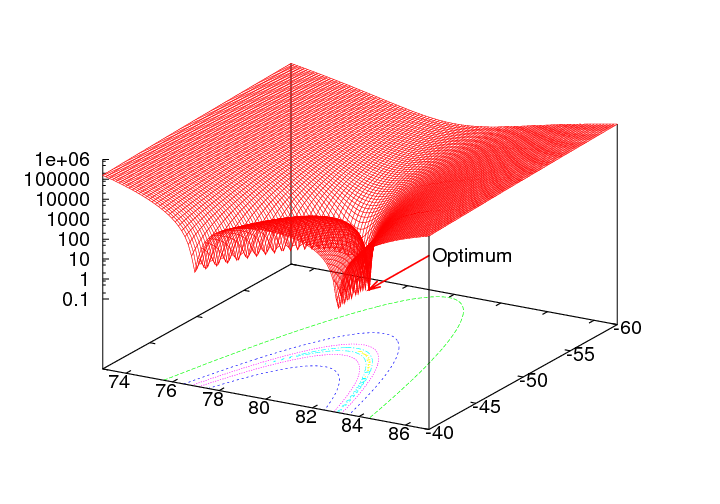
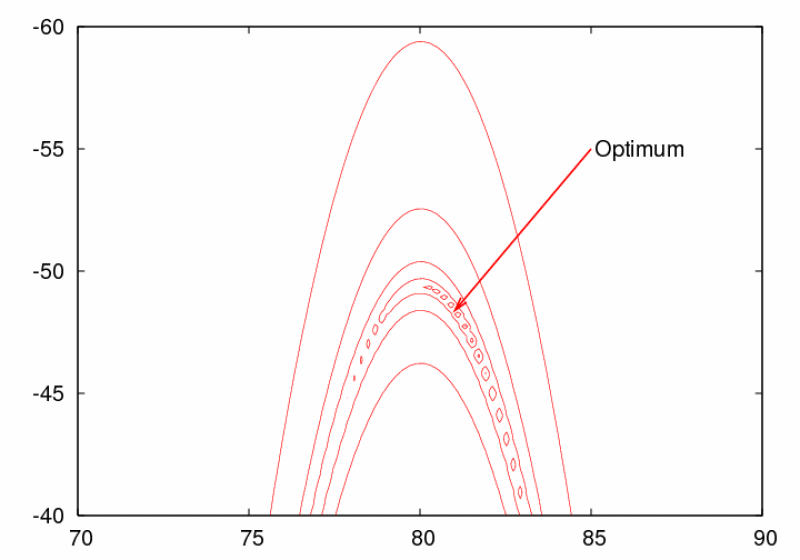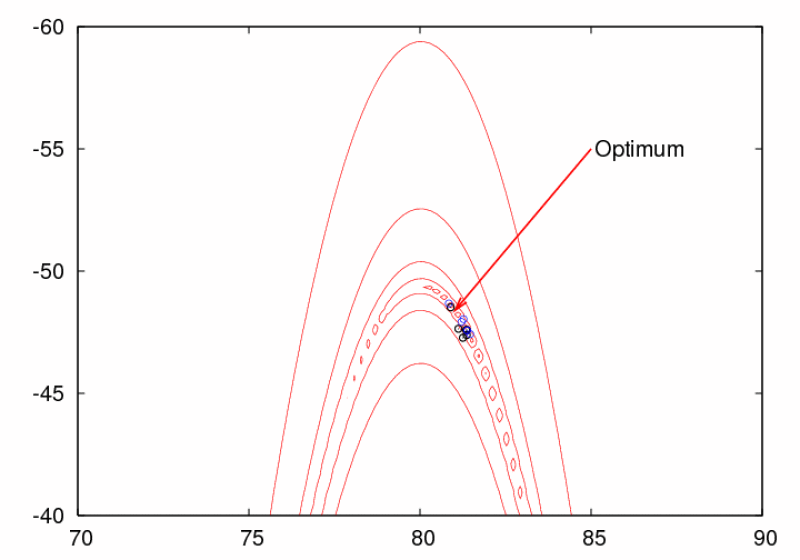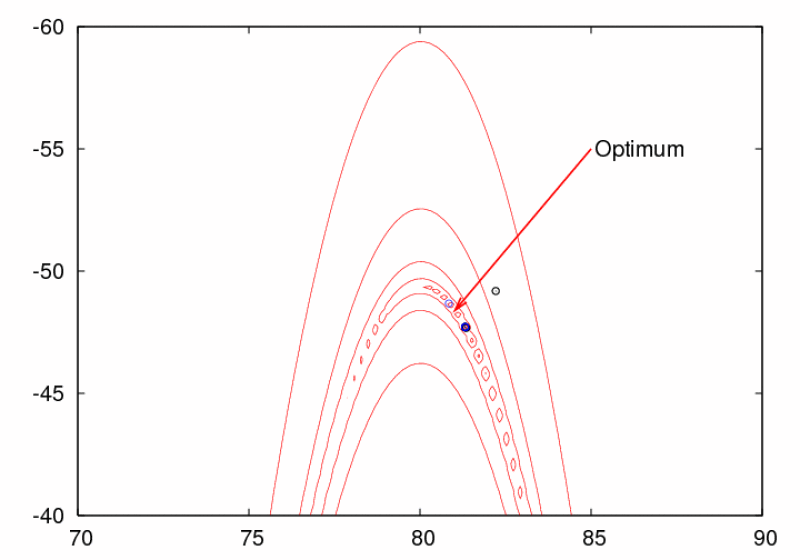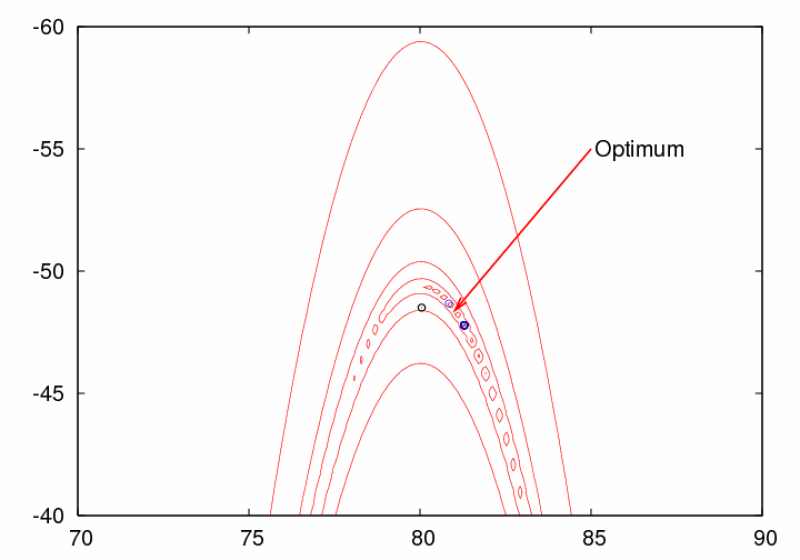
The figure above shows a swarm of 6 particles solving a two-dimensional displaced Rosenbrock's function. The swarm is using a fully connected topology (known as gbest) and the so-called constriction factor (= 0.729). The blue dots show where the particles' previous best positions are (called pbest). The black dots show the particles' current position. It is also shown where the true optimum is located.
Some introductory slides can be found here.
Swarm intelligence has also been used in machine learning. While most swarm intelligence applications for machine learning are based on search and optimization algorithms (see Martens et al. (2011)), there are methods specifically designed for pattern recognition. One of these methods is called Ant-based Clustering (Handl and Meyer, 2007), in which the data vectors to be clustered are seen as “pellets” and are randomly placed on a toroidal grid together with some agents. These agents move around at random picking up or dropping pellets with a probability that depends on the agents’ locally-perceived pellet density and similarity. Pellets in areas of high density are rarely picked up, while isolated pellets are almost always picked up. Similarly, agents drop pellets with a high probability in areas of high density and almost never drop pellets in areas of low density. Through this process, larger clusters tend to grow while smaller ones tend to disappear. By adding a similarity measure that modulates the agents’ density perception, actual data clustering can be obtained. My contributions in this field are the study of inter-agent communication (Montes de Oca et al., 2005), and a hybrid algorithm that combines ant-based clustering with neural networks for unsupervised classification (Montes de Oca et al., 2005).
Further info:
Ant-based clustering is inspired by the aggregation behaviors exhibited by some termite and ant species. In actual implementations of these algorithms, agents (simulating ants or termites) move over a toroidal square grid on which there are data objects. Agents pick up a data object with high probability if it is not surrounded by other similar data objects. By the same token, agents drop data objects on any free location surrounded by similar objects to the one they are carrying. For more information go to the publications section.

In this figure, you can observe the development of the clustering process as performed by simulated ants. In this example, there are three real clusters that can be identified by differences in color. It can be seen how ants are capable of identifying them correctly. It should be noted that ant-based clustering algorithms do not require the user to specify the number of clusters to retrieve. In some cases, ant based clustering algorithms are capable of identifying the correct number of clusters existing in a data set.
A second aspect of machine learning that I work on is reinforcement learning. I have explored learning at the individual and at the collective levels. To learn at the individual level, agents compare the outcomes of their behavioral adaptations in order to choose the one that best contributes to the attainment of a desired collective-level behavior. Learning at the swarm level means that the memory of the trial and error process resides in the whole swarm distributed among the agents, which do not compare the outcomes of their behavioral adaptations.
Appealing as it is, the idea of letting each agent individually learn its behavior in order to obtain a desired collective-level behavior is difficult on a practical level. The main problem is that agents not only must adapt to their environment, but they also have to cope with the behavioral changes of other learning agents. In many cases, this situation creates interferences between agents, and ultimately hinders the system’s ability to satisfactorily perform the assigned task, especially when the population is large, as it is in a swarm (Panait and Luke (2005) discuss the problems encountered in multi-agent learning). To tackle this problem, I proposed a technique called incremental social learning (ISL) (Montes de Oca and Stützle, 2008b; Montes de Oca, 2011). It consists of two key elements: a population of agents that grows larger over time and social learning. A population that starts small and grows over time suffers less from interference and social learning allows newly added agents to acquire knowledge about their environment from older agents without incurring the costs of acquiring that knowledge by themselves. I have successfully applied ISL to multi-agent systems (Montes de Oca and Stützle, 2008b) and to PSO algorithms (Montes de Oca et al., 2011b). In both cases, the performance of the swarm improved substantially. Thus, by alleviating some of the problems encountered when a swarm is composed of learning agents, ISL contributes to the practical development of swarm intelligence systems.
Recently, I have been working on collective learning in scenarios in which a swarm has to learn which of two alternative actions improves its performance (Montes de Oca et al., 2010, 2011a; Montes de Oca, 2013b). I have explored two mechanisms to achieve this goal. One of these mechanisms is based on the majority-rule opinion formation model (Krapivsky and Redner, 2003) and the other one is based on the exponential smoothing equation (Montes de Oca et al., 2013). These works are related to a branch of statistical physics called opinion dynamics (Castellano et al., 2009). These mechanisms have applications in multi-robot systems in scenarios where robot actions can be modeled as opinions and the goal is to find the best of a number of available actions. The opinion dynamics of these mechanisms play the role of the action exploration mechanism commonly found in traditional learning algorithms. As far as I know, I am the first to propose opinion dynamics as the principal mechanism for collective learning. This work enables the application of ideas and tools developed by the statistical physics community in the swarm intelligence field. This work also contributes to the practical development of swarm intelligence systems and to the better understanding of the processes that allow complex collective phenomena to emerge.
Further info:
A swarm robotics system is a multi-robot system in which robots coordinate their actions using swarm intelligence principles. For more information go to the publications section.
This video shows the collective decision-making process that results from
the application of the majority-rule opinion dynamics model with differential
latency as described here.
The environment consists of two areas between which the robots must
transport objects collectively. These two areas are at the top and bottom parts
of a video frame. Connecting these two areas there are two corridors of
different length. Each team of robots must choose between these two corridors to
go to the target area. At each decision point, there is an LED that helps robots
know in which direction to turn. For simplcity, objects are removed from the
simulation as soon as they are transported to the target area. Something similar
happens with robots once they go back to the starting area.
In this
example, a population of 32 robots and 8 teams are used. Initially, 16 robots
prefer the left path and 16 robots prefer the right path. Every time a team is
formed (at random), the local majority determines which path the team will
follow. At the end of the simulation the population achieves consensus on the
left path. Note: The speed of the video is 4 times the normal speed of the
simulation.
Outlook
Complex systems are ubiquitous in the natural and social worlds. However, in the engineering world we prefer simple systems, which can be fully explained using a reduced set of well-understood principles (e.g., Newton’s laws, differential equations). An equivalent set of principles to explain and predict the behavior of complex systems is the subject of most research in the field. These efforts are important because we are beginning to realize that some of our biggest problems have analogues in the natural world and we are continuously discovering that the solutions to those natural problems are provided by complex systems (see e.g., Bettencourt et al. (2007)). Hence, understanding complexity may be key for the development of our next-generation solution techniques. In the computing world, artificial intelligence has been the provider of next-generation solution techniques since it was established. Some decades ago, nature-inspired techniques, such as neural networks, reinvigorated interest in the field. Interestingly, neural networks may actually be regarded as an example of a complex system. I believe that the second boost of this renewed interest in artificial intelligence can be a unified approach to the study of complex systems and artificial intelligence. So far, search & optimization, learning, pattern recognition, and robotics have been the most popular application areas of complex systems phenomena but other applications are also possible. At the same time, our understanding of complex systems is still in its infancy. Therefore, the research program that I want to establish will also investigate possible ways in which artificial intelligence methods can be used to help in the modeling, simulation, and output data processing in order to advance our understanding of complex systems.
References
Beni, G. and Wang, J. (1993). Swarm Intelligence in Cellular Robotic Systems. In Paolo, D. et al., editors, Proceedings of the NATO Advanced Workshop on Robots and Biological Systems, page 2. Springer, Berlin, Germany.
Bettencourt, L. M. A., Lobo, J., Helbing, D., Kühnert, C., and West, G. B. (2007). Growth, innovation, scaling, and the pace of life in cities. PNAS, 104(17):7301–7306.
Bonabeau, E., Dorigo, M., and Theraulaz, G. (1999). Swarm Intelligence: From Natural to Artificial Systems. Santa Fe Institute Studies on the Sciences of Complexity. Oxford University Press, New York.
Castellano, C., Fortunato, S., and Loreto, V. (2009). Statistical physics of social dynamics. Reviews of Modern Physics, 81(2):591–646.
Couzin, I. D. (2007). Collective Minds. Nature, 445(7129):715.
Dorigo, M. and Stützle, T. (2004). Ant Colony Optimization. Bradford Books. MIT Press, Cambridge, MA.
Grassé, P.-P. (1959). La reconstruction du nid et les coordinations interindividuelles chez Bellicositermes natalensis et Cubitermes sp. La théorie de la stigmergie: Essai d’interprétation du comportement des termites constructeurs. Insectes Sociaux, 6(1):41–80.
Handl, J. and Meyer, B. (2007). Ant-based and swarm-based clustering. Swarm Intelligence, 1(2):95–113.
Kennedy, J. and Eberhart, R. (1995). Particle Swarm Optimization. In Proceedings of IEEE International Conference on Neural Networks,
pages 1942–1948. IEEE Press, Piscataway, NJ.
Krapivsky, P. L. and Redner, S. (2003). Dynamics of Majority Rule in Two-State Interacting Spin Systems. Physical Review Letters, 90(23):238701, 4 pages.
Le Bon, G. (1895). La psychologie des foules (trans. The Crowd: A Study of the Popular Mind) . Ancienne Librarie Germer Bailliére, Paris, France.
Liao, T., Molina, D., Stützle, T., Montes de Oca, M. A., and Dorigo, M. (2012). An ACO Algorithm Benchmarked on the BBOB Noiseless Function Testbed. In Auger, A. et al., editors, Proceedings of the Workshop on Black-Box Optimization Benchmarking of the Genetic and Evolutionary Computation Conference (GECCO 2012), pages 159–166. ACM Press, New York.
Liao, T., Montes de Oca, M. A., Aydin, D., Stützle, T., and Dorigo, M. (2011). An Incremental Ant Colony Algorithm with Local Search for Continuous Optimization. In Krasnogor, N. et al., editors, Proceedings of the Genetic and Evolutionary Computation Conference (GECCO 2011), pages 125–132. ACM Press, New York, NY.
Liao, T., Socha, K., Montes de Oca, M. A., Stützle, T., and Dorigo, M. (2013). Ant Colony Optimization for Mixed-Variable Optimization Problems. IEEE Transactions on Evolutionary Computation. In press.
Martens, D., Baesens, B., and Fawcett, T. (2011). Editorial survey: swarm intelligence for data mining. Machine Learning, 82(1):1–42.
Miller, R. C. (1921). The Mind of the Flock. The Condor, 23(6):183–186.
Minsky, M. (1986). The Society of Mind. Simon and Schuster, New York.
Montes de Oca, M. A. (2011). Incremental Social Learning in Swarm Intelligence Systems. PhD thesis, Université Libre de Bruxelles.
Montes de Oca, M. A. (2013a). Incremental Social Learning in Swarm Intelligence Algorithms for Continuous Optimization. In Madani, K.
et al., editors, Computational Intelligence. Revised and Selected Papers of the International Joint Conference, IJCCI 2011., pages 31–45. Springer, Berlin, Germany.
Montes de Oca, M. A. (2013b). Social Reinforcement for Collective Decision-Making Over Time. In Proceedings of the 1st Multidisciplinary Conference on Reinforcement Learning and Decision Making. Online proceedings. To appear.
Montes de Oca, M. A., Aydin, D., and Stützle, T. (2011). An Incremental Particle Swarm for Large-Scale Continuous Optimization Problems: An Example of Tuning-in-the-loop (Re)Design of Optimization Algorithms. Soft Computing, 15(11):2233–2255.
Montes de Oca, M. A., Ferrante, E., Mathews, N., Birattari, M., and Dorigo, M. (2010). Opinion Dynamics for Decentralized Decision-Making in a Robot Swarm. In Dorigo, M. et al., editors, LNCS 6234. Proceedings of the Seventh International Conference on Swarm Intelligence (ANTS 2010), pages 251–262. Springer, Berlin, Germany.
Montes de Oca, M. A., Ferrante, E., Scheidler, A., Pinciroli, C., Birattari, M., and Dorigo, M. (2011a). Majority-Rule Opinion Dynamics with Differential Latency: A Mechanism for Self-Organized Collective Decision-Making. Swarm Intelligence, 5(3–4):305–337.
Montes de Oca, M. A., Ferrante, E., Scheidler, A., and Rossi, L. F. (2013). Binary Consensus via Exponential Smoothing. In Glass, K. et al., editors, LNICST 126. Proceedings of the Second International Conference on Complex Sciences: Theory and Applications (COMPLEX
2012), pages 244–255. Springer, Berlin, Germany.
Montes de Oca, M. A., Garrido, L., and Aguirre, J. L. (2005). An hybridization of an ant-based clustering algorithm with growing neural gas networks for classification tasks. In Haddad, H., Liebrock, L. M., Omicini, A., and Wainwright, R. L., editors, Proceedings of the 20th Annual ACM Symposium on Applied Computing. SAC 2005, pages 9–13, New York. ACM Press.
Montes de Oca, M. A., Garrido, L., and Aguirre, J. L. (2005). Effects of Inter-agent Communication in Ant-based Clustering Algorithms: A Case Study on Communication Policies in Swarm Systems. In Gelbukh, A. et al., editors, LNAI 3789. Proceedings of the Fourth Mexican International Conference on Artificial Intelligence (MICAI 2005), pages 254–263. Springer, Berlin, Germany.
Montes de Oca, M. A., Peña, J., Stützle, T., Pinciroli, C., and Dorigo, M. (2009a). Heterogeneous Particle Swarm Optimizers. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC 2009), pages 698–705. IEEE Press, Piscataway, NJ.
Montes de Oca, M. A. and Stützle, T. (2008a). Convergence Behavior of the Fully Informed Particle Swarm Optimization Algorithm. In Keijzer, M. et al., editors, Proceedings of the Genetic and Evolutionary Computation Conference (GECCO 2008), pages 71–78. ACM Press, New York.
Montes de Oca, M. A. and Stützle, T. (2008b). Towards Incremental Social Learning in Optimization and Multiagent Systems. In Rand, W. et al., editors, Workshop on Evolutionary Computation and Multiagent Systems Simulation of the Genetic and Evolutionary Computation Conference (GECCO 2008), pages 1939–1944. ACM Press, New York.
Montes de Oca, M. A., Stützle, T., Birattari, M., and Dorigo, M. (2006). A Comparison of Particle Swarm Optimization Algorithms Based on Run-Length Distributions. In Dorigo, M. et al., editors, LNCS 4150. Proceedings of the Fifth International Workshop on Ant Colony Optimization and Swarm Intelligence (ANTS 2006), pages 1–12. Springer, Berlin, Germany.
Montes de Oca, M. A., Stützle, T., Birattari, M., and Dorigo, M. (2009b). Frankenstein’s PSO: A Composite Particle Swarm Optimization Algorithm. IEEE Transactions on Evolutionary Computation, 13(5):1120–1132.
Montes de Oca, M. A., Stützle, T., Van den Enden, K., and Dorigo, M. (2011b). Incremental Social Learning in Particle Swarms. IEEE Transactions on Systems, Man and Cybernetics - Part B: Cybernetics, 41(2):368–384.
Panait, L. and Luke, S. (2005). Cooperative Multi-Agent Learning: The State of the Art. Autonomous Agents and Multi-Agent Systems,
11:387–434.
Seeley, T. D. (2010). Honeybee Democracy. Princeton University Press, Princeton, NJ.
Surowiecki, J. (2005). The Wisdom of Crowds. Anchor Books, New York.
Trianni, V., Tuci, E., Passino, K. M., and Marshall, J. A. R. (2011). Swarm Cognition: an interdisciplinary approach to the study of self-organising biological collectives. Swarm Intelligence, 5(1):3–18.